The Road Ahead week3 Sequential Logic

Posted on | In ,

“The great wall is made by blocks”

简介

为何要引入时间概念

目前为止，我们所讨论的电路都是直接输入输出，没有考虑时间因素，这种电路又叫做组合电路，从现在开始，我们要考虑引入时间影响。例如有如下场景：

  • 在不同时间下使用相同的硬件
1
2
3
# 输入改变，输出也应当随之变化
for i in 1 .. 100:
    a[i] = b[i] + c[i]
  • 记录状态，例如内存/计数器等
1
2
for i in 1 .. 100:
    sum = sum + i
  • 处理速度时，尽管我们希望我们的电路无延迟，但是实际过程肯定是有的，所以我们需要考虑计算机中器件的延迟

时钟

离散的时钟信号如下所示：

图片名称

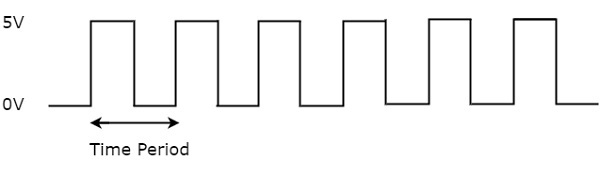
在一个时钟周期中，输入与输出是固定的，在不同时钟周期可能会有变化，且由于器件延迟，变化并不是实时的，会有一个变化时间。选择时钟信号的频率时，我们需要确保能够满足器件的响应时间

图片名称

组合逻辑和时序逻辑的区别

  • 组合逻辑：out[t] = func(in[t])
  • 时序逻辑：out[t] = func(in[t-1])，或者state[t] = func[state[t-1]]

触发器

触发器介绍

现在，让我们实现一个触发器功能，即在两种状态间进行翻转的电路，并最终实现以下逻辑：

1
2
3
4
5
6
state[t] = func[state[t-1]]

t0: a
t1: b = func(a)
t2: c = func(b)
t3: d = func(c)

为了实现上述功能，我们需要考虑下面这样一个部件：

  • 缺失的部件：t-1时刻的信息可以在t时刻使用
  • 在t-1时刻的末尾，该部件可以有两种状态，记忆0或者记忆1
  • 这个部件在可能的状态间进行切换，这种器件叫做触发器

该器件的示意图和信号如下所示：

图片名称

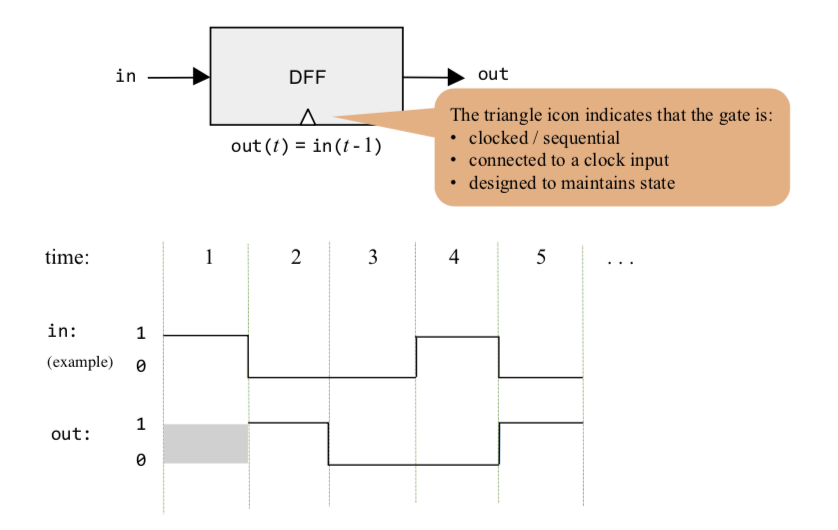
其中尖角代表时钟信号，根据状态转移函数，可知out为前一时刻的in，实际就是将输入信号滞后一个时钟周期输出

触发器实现

使用与非门实现触发器一般需要如下两个步骤：

  • 通过闭环实现一个时间无关的触发器
  • 通过一个”主从”结构实现时间的隔离

通过组合多个触发器，我们能够实现比较复杂的时序逻辑

图片名称

在本课程中，触发器是作为基本元件提供的

寄存器

寄存器的目标是永久性存储一个值，直到载入一个新值为止

图片名称

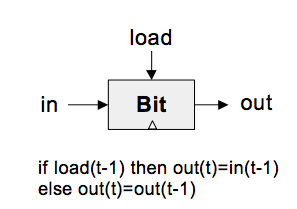
逻辑如下：

1
2
3
4
if (load[t-1])
    out[t] = in[t-1]
else
    out[t] = out[t-1]

我们可以利用一个Mux和一个D触发器实现上面的电路：

图片名称

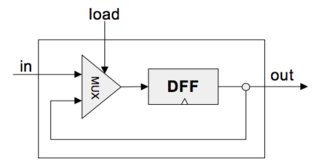
从电路图中我们能够看出，DFF总是保存输入的bit，但是寄存器仅在load = true时保存in，DFF仅能在一个时间单位保存信息，但是寄存器能够在多个时间单位中保存。

寄存器有两个重要属性：

  • 寄存器位宽
  • 寄存器状态：保存在寄存器中的值

需要注意的是，寄存器的状态和寄存器的输出值是有差异的，一个CPU时钟周期内，如果设置load为1，那么寄存器状态会在前半个周期就改变，而寄存器输出的值直到完整的一个周期才会发生变化。

内存单元

内存结构

内存单元实际上就是寄存器组，假设一个内存块包含$n$个寄存器，那么内存的地址就是从0到$n-1$，对于任意时刻，内存中只会有一个寄存器被选中

mem unit

RAM是一个时序芯片，包含了时间行为：

1
2
3
4
5
6
7
8
// Let M stands for the state of the selected register
if load then {
    M = in
    // from the next cycle onward:
    out = M        // The output of RAM is slower than input
} else {
    out = M
}

内存读写

读操作：

  • set address = i

输出的结果即为寄存器$i$的值

写操作

1
2
3
set address = i
set in = v
set load = 1

Counter

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * A 16-bit counter with load and reset control bits.
 * if      (reset[t] == 1) out[t+1] = 0
 * else if (load[t] == 1)  out[t+1] = in[t]
 * else if (inc[t] == 1)   out[t+1] = out[t] + 1  (integer addition)
 * else                    out[t+1] = out[t]
 */

CHIP PC {
    IN in[16],load,inc,reset;
    OUT out[16];

    PARTS:
    // Put your code here:
    Inc16(in = dout, out = pcInc);
    Mux16(a = dout, b = pcInc, sel = inc, out = out1);
    Mux16(a = out1, b = in, sel = load, out = out2);
    Mux16(a = out2, b = false, sel = reset, out = out3);

    Register(in = out3, load = true, out = out, out = dout);

}

参考文献

0%